2018年 長野開催

練習問題:Q1
5~100の間の数値を、5で割って、余りが2もしくは4になる数値の合計を解答してください。
- 解答
- 2014
練習問題:Q3
 (1)が縦または横につながっている一番小さい塊は、何塊ありますか?
(1)が縦または横につながっている一番小さい塊は、何塊ありますか?
テンプレートを使用して解答してください。

 (1)/
(1)/ (0)
(0)例

 (1)/
(1)/ (0)
(0) (1)の一番小さい塊は、3個の塊です。その塊が4個あります
(1)の一番小さい塊は、3個の塊です。その塊が4個あります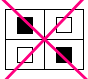
- ※斜めに接するものは塊としてカウントしません
- 解答
- 3
ダウンロード

- 解答
- 3

何日滑れる?
「白駒の池」と呼ばれる湖があります。標高2,100m以上の湖としては日本最大の天然湖と言われており、かつてはスケート選手がここで合宿をしていたそうです。
平均気温が0℃以下の日に限り、スケート練習ができます。練習ができる日は、1ヶ月(30日)間に何日あるでしょうか?
1ヶ月の1日毎の平均気温が配列で与えられます。練習できる日数を回答してください。
※テンプレートを使用して回答して下さい。
配点:100点
ダウンロード

- 解答
- 15
例
- 例題
- {13, 13, 5, 14, 0, 3, 11, 11, -5, 7, 5, 9, 2, -3, 14, 4, 2, 4, 13, 10, -5, 14, 14, 10, 6, 7, 4, 4, 3, -4}
- 解答
- 5
★この問題が解けない方へのヒント★
※このコンテストではWeb上での検索が認められています。プログラムの書き方が分からない場合は検索しましょう!
※下記の通りに解く必要はありません。考え方の1つです。
- 配列を初期値として登録しましょう。
- 30日分の繰り返し処理を書きましょう。
- その日の平均気温が0℃以下であれば「練習できる日数」を増やしましょう。
- 最後に「練習できる日数」を出力しましょう。

八ヶ岳の神話
ここ長野県に佇む八ヶ岳には、次のような神話があります。
---------------------------------------------
むかーしむかし、八ヶ岳はとても大きな一つの山でした。
ある日、八ヶ岳が富士山と背比べをしたところ、僅差で勝利し、八ヶ岳はとても喜んでいました。
しかし負けた富士山は怒りに任せて、なんと八ヶ岳を蹴り飛ばしてしまったのです。
その結果、八ヶ岳は八つの峰に割れてしまいました。
それを見た八ヶ岳の妹である蓼科山は、悲しさのあまり涙を流しました。
その涙が川となり、流れ溜まって諏訪湖になったということです。
---------------------------------------------
さて、この神話のように「YATSUGATAKE」が「FUJISAN」に蹴り飛ばされて「Y」「AT」「S」「U」「GAT」「A」「K」「E」の八つの部品に分かれ、文字列の中に紛れてしまいました。
あなたの力で文字列から八つの部品を見つけて、それぞれの位置を教えてください。
- どの部品も、文字列の中に一つだけ存在します。
- 文字列は「0文字目」からスタートします。
- 回答は「Y」「AT」「S」「U」「GAT」「A」「K」「E」の順に、カンマ区切りで出力してください。
- 「GAT」「AT」は、それぞれ最初の文字の位置を解答してください。
- 「A」と「AT」と「GAT」は、それぞれ別の物としてカウントしてください。
例えば、「AT」は「GAT」の中に含まれるため、例題において「AT」の位置を「3」と解答することも出来ますが、それは間違いとします。
※テンプレートを使用して回答して下さい。
配点:200点
ダウンロード

- 解答
- 22,61,9,3,55,67,40,32
例
- 例題
- CQGATWSMATFYVUIAHLKE
- 解答
- 11,8,6,13,2,15,18,19


正方形作成ゲーム
あなたは友人が考案した「正方形作成ゲーム」で遊んでいます。考案者を除くとあなたは世界初のプレイヤーです。
このゲームを考案した友人は「各盤面に対する最高スコアを算出するプログラムを作成したい」と思ったのですが、実装方法がわからなかったため、プログラミング能力の高いあなたに相談しました。
【「正方形作成ゲーム」のルール】
- 盤面は10x10に並べられた正方形のマスで構成されています。
- 各マスには、0~9の数のいずれかが、一つずつ書かれています。
- あなたはマスの中心を頂点とする正方形を作成することができます。
- 正方形を作成した際、以下の規則でスコアが変化します。
- 既に作成した正方形と位置も大きさも等しい正方形が作成された場合、スコアは変化しない。
- 盤面に対して斜めの正方形が作成された場合、スコアは変化しない。
- 正方形の頂点のマスに書かれた数に一つでも0がある場合、スコアは変化しない。
- 上記以外の場合、正方形の頂点のマスに書かれた数の合計がスコアに加算される。
- 初期スコアは0点です。
- 正方形は、いくつでも作成することができます。
与えられた盤面に対して得ることができる最高スコアを求めてください。
3つの盤面データが与えられます。それぞれに対する答えをカンマ区切りで回答してください。
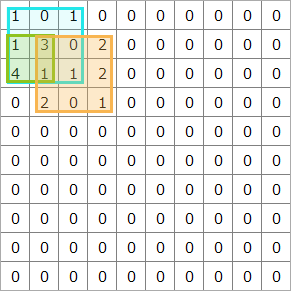
例えば、上記の盤面の場合、3つの正方形を作成して、24点を得ることができます。
(※図に描いた正方形は数字を読みやすくするためにサイズや位置を調整していますが、頂点は各マスの中央である必要があります。)
・1+1+4+1=7点加算
・1+3+4+1=9点加算
・3+2+2+1=8点加算
合計:24点
※25点以上取ることはできないため、この盤面における最高スコアは24点です。
※テンプレートを使用して回答して下さい。
配点:300点
ダウンロード

- 解答
- 1439,3150,10260

ロボットで迷路を駆け抜けろ!
あなたが所属するロボコンチームは、次のコンテストに向けて、迷路を走破するロボットを作成しています。
日々の努力により、必要最低限の動作はするようになりました。「ロボットの進行方向を、反時計回りに回転させることができない」という明らかな欠陥はあるものの、与えられた迷路を走破することが可能です。
あなたは、このロボットが迷路を走破するのにどれだけの時間がかかるのかを調べようと考えました。
【迷路の例】

各マスは正方形です。スタート(S)、ゴール(G)、白いマスは通過可能で、各マスの中心に停止可能です。黒いマスは進入不可能です。また、迷路の外に移動することは禁止されています。
上図の迷路は下記の文字列で表されます。
"5 4 0000S1001010100001G1"
つまり、"縦マス数(1桁の数字) 横マス数(1桁の数字) 一番上から一番下まで各行の左から右に順番に並べられた各マスの情報(0,1,S,Gから構成されていて、SとGは一つずつ含まれる)" という形式です。
※迷路には、上図の左下のマスのように到達不可能なマスが存在する場合があります。スタートからゴールへは到達可能です。
【ロボットの操作に関する説明】
- 以下の三つの操作が可能です。
- 停止中のロボットの向きを、時計回りに45度回転 (3秒で回転完了とともに停止)
- 停止中のロボットを、前方のマスに移動 (5秒で移動完了とともに停止)
- 停止中のロボットを、後方のマスに移動 (7秒で移動完了とともに停止)
- 斜めに移動する場合、移動前のマスと移動後のマスの両方に接するマスも通過可能なマスである必要があります。

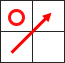
ロボットはスタートにいて、図の上の方向を向いて停止しています。
この状態から、ゴールに停止するまで最短何秒かかるでしょうか。ゴールに停止時のロボットの向きは問いません。
3つの迷路が与えられます。それぞれの迷路に対する答えをカンマ区切りで答えてください。
※テンプレートを使用して回答して下さい。
配点:400点
ダウンロード

- 解答
- 127,225,255
例題
- 例題
- "5 4 0000S1001010100001G1"
"2 2 1GS0"
"3 5 S00000101000G00" - 解答
- 66,24,30

東京へ帰りたい
東京都内のある小学校のプログラミングクラブが、茅野(ちの)市で行われるプログラムコンテストに保護者と一緒に参加しました。無事にコンテストは終了し、その夜は近くのロッジに宿泊したのですが、翌朝大変困ったことが起こりました。なんとチャーターしていた帰りの貸切バスが、中央自動車道の事故渋滞に巻き込まれてしまい、迎えに来られないというのです。このままでは、家まで帰ることができません。
ロッジの最寄り駅である茅野駅までたどり着けば、特急あずさで東京へ帰ることができるのですが、ロッジの近くには路線バスが走っていません。また、タクシー会社に電話したところ、タクシーは全車予約済みで今日は呼ぶことができないことが分かりました。
困り果てていると、幸運なことにロッジの人が車を貸してくれると言うではありませんか。さらに茅野駅前のレンタカー会社に電話をしたところ、1台の軽トラックを借りられることも分かりました。何人かの保護者は運転免許を持っています。2台の車を最大限に活用すれば、全員無事に駅まで帰れそうですが、誰かが駅に行かなければ軽トラックは借りられませんし、ロッジから借りた車は、最後にはロッジに返さなければなりません。
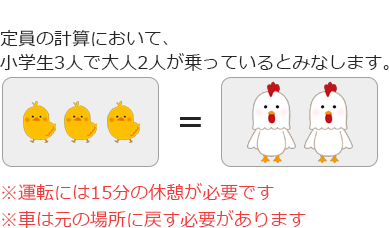
ロッジで借りられる車は普通乗用車で5人乗り、駅で借りられる軽トラックは2人乗りです。乗用車の定員は、小学生3人を大人2人分として計算することができます。例えば、乗用車には最大で[大人5人]、[大人3人+子供3人]、[大人1人+子供6人]、というような組み合わせで乗車することができます。
乗用車では駅まで片道30分かかります。軽トラックでは信号がない急峻な林道を通ることで、駅まで片道15分でたどり着くことができます。最初、乗用車はロッジにあり、軽トラックは駅にあります。使用後は2台とも元の場所に返さなければいけません。
一人の運転手がずっと運転することはできません。片道を運転したら、15分休憩が必要です。なお乗車して移動している最中であっても、運転していなければ休憩していると見なせます。
コンテストの参加者は、小学生がX人、保護者がY人、保護者のうちで運転できる人がZ人、として
{X, Y, Z}
のように与えられます。駅まで全員がたどり着き、車を元の場所に戻すのに必要な最短時間を求めてください。

※テンプレートを使用して回答して下さい。
配点:500点
ダウンロード

- 解答
- 135,210,420
例題
- 例題
- {1, 2, 2} // 小学生1人、保護者2人(そのうち運転可能なのは2人)
{4, 2, 2} // 小学生4人、保護者2人(そのうち運転可能なのは2人)
{5, 5, 3} // 小学生5人、保護者5人(そのうち運転可能なのは3人) - 解答
- 90,90,135