開催終了したイベント：2021年3月6日(土)　オンライン開催

title line
Q1

スペアはいくつ？？
N君はボウリングで遊んでいます。
下記にN君のボウリングで倒したピンの数をまとめた表があります。
スペアはいくつありますか？？
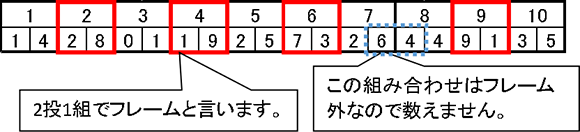
問題イメージ図
この問題における「スペア」とは赤枠のように2投(フレーム)の合計が10になったときの事を言います。
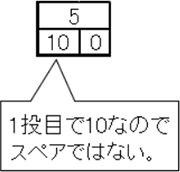
ただし各フレームにおいて1投目で10になった場合はストライクとなりスペアとは見なしません。
問題イメージ図
入力は「倒したピンの数」が配列で与えられます。配列の要素数は20です。
3パターンの入力があります。それぞれに対する答えを求め、カンマ区切りで答えてください。

※テンプレートを使用して解答してください。
配点：100点

Q１のテンプレートを
ダウンロード ダウンロード
解答
4,5,5

例

例題
{1,4,2,8,0,1,1,9,2,5,7,3,2,6,4,4,9,1,3,5}
{10,0,1,2,3,5,6,2,10,0,9,1,0,3,2,7,3,5,2,1}
{0,10,3,7,5,5,2,1,0,10,3,1,6,4,2,1,3,1,3,3}
解答
4,1,5
Q2

玉落とし装置
空中に横に長い装置が設置されています。
この装置には複数の玉が設置されています。
地上には複数の穴があります。
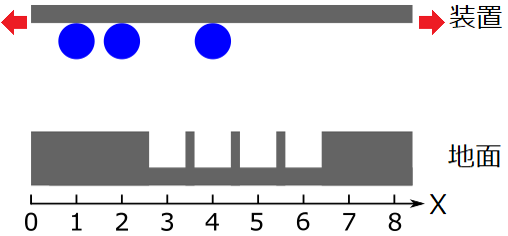
問題イメージ図
装置は左右に動かすことが可能です。
装置を動かすと全ての玉も相対位置を保ったまま左右に動きます。
「落下」ボタンを押すと全ての玉が同時に真下に落下します。
落下した玉は、地上に同じX座標の穴がある場合にその穴の中に入ります。
玉と穴の位置情報が与えられるので、穴に入る玉の最大数を答えてください。

入力は整数列として与えられます。
この整数列は玉と穴の位置情報を表していて、
{1つ目玉のX座標, 2つ目の玉のX座標, ......, 最後の玉のX座標, 0, 1つ目の穴のX座標, 2つ目の穴のX座標, ......, 最後の穴のX座標, 0}
という形式となっています。
玉の数は100個以下です。各玉のX座標は互いに異なり、値は1以上200以下で昇順になっています。
穴の数は150個以下です。各穴のX座標は互いに異なり、値は1以上200以下で昇順になっています。

例題の1つ目の入力が問題文中の図に対応しています。ご覧ください。
5パターンの入力があります。それぞれに対する答えを求め、カンマ区切りで答えてください。

※テンプレートを使用して解答してください。
配点：200点

Q２のテンプレートを
ダウンロード ダウンロード
解答
9,18,36,79,55

例

例題
{1,2,4,0,3,4,5,6,0}
{1,4,5,0,1,2,0}
{1,2,4,0,1,3,4,0}
{2,3,6,7,9,10,0,5,7,9,11,13,15,0}
{4,11,14,15,23,28,29,36,43,45,48,52,55,62,63,68,91,99,102,108,115,116,122,124,148,163,171,186,190,198,0,5,7,12,14,15,17,38,46,51,52,60,66,67,68,69,72,73,80,93,96,101,102,103,105,107,109,113,115,116,117,119,123,125,132,136,138,141,149,150,154,156,161,170,180,187,189,192,195,198,200,0}
例題の解説
1つ目の入力は問題文中の図と対応しています。この場合、装置をX軸正の向きに2動かしてから「落下」ボタンを押すことで3つの玉が全て穴に入るため、答えは3です。
2つ目の入力は装置をX軸負の向きに3動かすことで2つの玉を穴に入れることが出来ます。このときが最大で、答えは2です。
3つ目の入力はもしも装置を180度回転できれば3つ全て入れることができるのですが、その操作はできません。例えば装置を動かさずに落下ボタンを押すことで2つの玉を穴に入れることはできます。答えは2です。
解答
3,2,2,3,13
Q3

球の行方は？？
20x20の格子状の盤面に球を転がします。球は盤面のマス目に従って縦方向あるいは横方向に転がり、途中で止まることはありません。盤面の途中に斜め45度の角度で板が立ててあり、この板に当たると球は90度進行方向を変えます。球が当たった板は倒れて消失します。球は板のどちら側に当たっても進行方向を変えることができ、このときに板の厚みや球の直径を考慮する必要はありません。

盤面の外に球が落下すると、次の球を転がします。盤面左端から右方向に球を10個転がし、最後の1個が落下する地点を答えてください。

盤面には左から右方向にABC…と記号が割り振られ、上から下方向に123…と数字が割り振られており、左上はA1、右下はT20と表記されます。解答は落下する球が最後に通過したマスで示すものとし、下図の例ではH20となります。

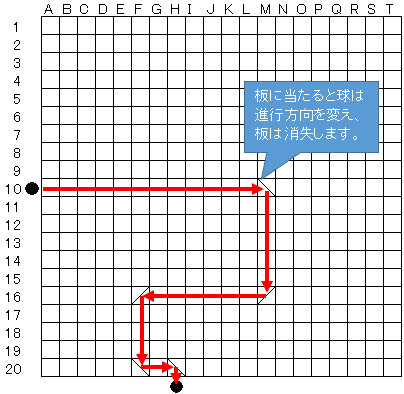
問題イメージ図
1個目の球はA1から、2個目の球はA2から、というように転がし、10個目のA10から転がされた球が落下する場所を解答してください。
盤面の情報はマス目を表す連続した文字列で与えられ、記号が大文字の場合は／、小文字の場合は＼、の向きの板が置いてあるものとします。
図の例では"m10F16M16f20h20"となります。

※テンプレートを使用して解答してください。
配点：300点

Q３のテンプレートを
ダウンロード ダウンロード
解答
A15,A4,K20

例題

例題
"m10F16M16f20h20"
"a1A2E3J4b5C6b7k8C9T10q11n12l13F14l15M16I17h18j19m20"
"c1f1Q1r1t1b2F2G2R2t2G3h3I3m3N3a4c4D4g4t4p5q5R5S5t5A6c6i6L6S6b7E7F7l7s7K8n8P8q8r8c9d9F9H9i9A10G10I10o10T10l11M11n11p11s11i12M12n12O12t12B13c13E13i13R13d14e14h14m14T14A15e15F15o15P15B16E16i16N16o16A17B17G17h17J17F18g18K18L18m18A19C19l19n19R19b20D20J20n20R20"
解答
H20,T1,A1
Q4

的当ての達人
あなたは的当てゲームをすることになりました。
弾を撃って的を倒すとポイントが獲得でき、その合計ポイントを競うゲームです。

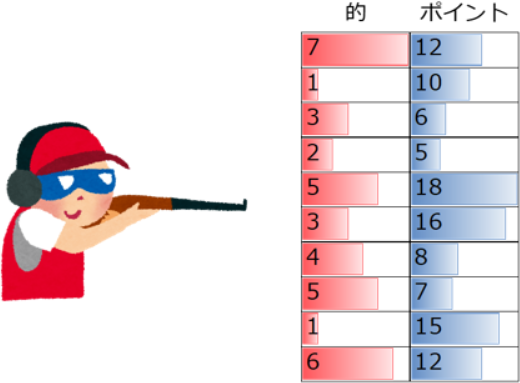
目の前には10枚の的があり、的毎に倒すために必要な弾の数が異なります。
i番目の的を倒すのに必要な弾数はb[i]です。
また、的毎に獲得出来るポイントが異なり、i番目の的を倒した時のポイントはp[i]です。
問題イメージ図
そしてこのゲームには以下のルールがあります。
・i番目とi+2番目を倒すと、自動的にi+1番目が倒れます。同時に2枚、または3枚の的を倒すことが可能です。
・弾は最初に10発所持しています。
・所持している弾の最後の1発（=所持している弾を使い切るタイミング）で倒した的のポイント分、弾が追加されます。
・最後の1発で倒した的が複数の場合、倒した的の合計ポイント分、弾が追加されます。
・弾を使い切るタイミングで的を倒せなかった場合、そこで終了となります。
・任意のタイミングで終了することも可能です。
・終了時に弾が残っていたら、残弾数をポイントとして加算することが出来ます(1発=1ポイント)。
・一度倒した的を狙うことはできません。また、的以外を撃つことはできません。
・一度的を撃ち始めたら、その的を倒すまで、他の的を撃つことはできません。

なお、あなたの撃った弾は100%的に当たります。
獲得できる最大の点数を求めてください。

入力は「的を倒すための弾数」と「倒したときのポイント」がそれぞれ配列で与えられます。
3パターンの入力があります。それぞれに対する答えを求め、カンマ区切りで答えてください。

※テンプレートを使用して解答してください。
配点：400点

Q４のテンプレートを
ダウンロード ダウンロード
解答
77,73,58

例題

例題
{7,1,3,2,5,3,4,5,1,6}
{12,10,6,5,18,16,8,7,15,12}

{1,2,3,4,5,6,7,8,9,10}
{10,9,8,7,6,5,4,3,2,1}

{11,8,2,10,6,8,2,13,3,9}
{12,1,3,6,2,1,9,13,10,4}
解答
151,72,70

↑TOP